
*이 글을 읽기전에 작성자 개인의견이 있으니, 다른 블로그와 교차로 읽는것을 권장합니다.*
1. 단항 선형 회귀
- 한 개의 입력이 들어가서 한 개의 출력이 나오는 구조
import torch
import torch.nn as nn # neural netowrk 딥러닝 클래스 모음
import torch.optim as optim # 학습알고리즘 보유
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
torch.manual_seed(2024)
x_train = torch.FloatTensor([[1],[2],[3]])
y_train = torch.FloatTensor([[2],[4],[6]])
print(x_train, x_train.shape)
print(y_train, x_train.shape)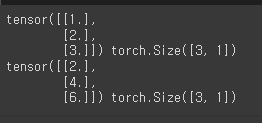
plt.figure(figsize=(6,4))
plt.scatter(x_train, y_train)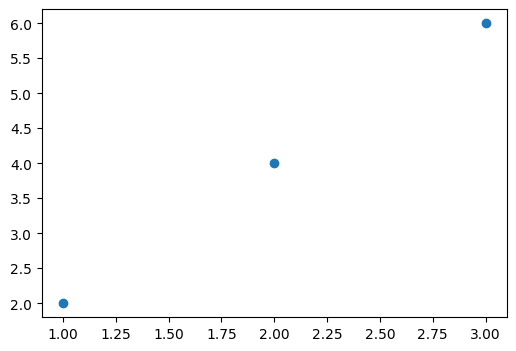
# y = wx + b
model = nn.Linear(1, 1)
print(model)
y_pred = model(x_train)
print(y_pred)
list(model.parameters()) # W: 0.0634, b: 0.6625
# y = 0.0634x + 0.6625
# x=1, 0.0634 + 0.6625 =0.7259
# x=2, (0.0634*2) + 0.6625 =0.7893
MSE( θ ^ )=E[(θ− θ ^ ) 2 ]
((y_pred - y_train) **2).mean()
loss = nn.MSELoss()(y_pred, y_train)
loss
2. 경사하강법(Gradient Descent)
- 비용함수의 값을 최소로 하는 W와 b를 찾는 알고리즘을 '옵티마이저 알고리즘'이라고 함
- 옵티마이저 알고리즘 중 가장 기본적인 기술이 경사하강법
- cost(w)의 최소값을 구하는 과정
- 편미분을 통해서 순간기울기(w)= Initial Weight를 구하고나서, Increment Step(학습률)으로 기울기를 순차적으로 수정, 최후에 Minimum cost(w)를 구함.
- z=f(x,y)=x^{2}+xy+y^{2}
- Step은 학습을 몇번 하는지 결정에 따라 달라짐.

- 옵티마이저 알고리즘을 통해 W와 bias를 찾아내는 과정을 '학습'
- 머신러닝 알고리즘에서 fit하는 과정과 동일
- 학습률(Learning rate): 한 번 W를 움직이는 거리(Increment Step)
# SGD(Stochasitc Gradient Descent)
# 랜덤하게 데이터를 하나씩 뽑아서 loss를 만듦
# 데이터를 뽑고 다시 데이터에 넣고 반복
# 원래 Gradient Descent는 데이터를 모두 들이붓고 수정하는데
# SGD는 랜덤하게 뽑아서 적용
# 빠르게 방향을 결정하는 것이 장점
optimizer =optim.SGD(model.parameters(), lr=0.01) # learning rate = 옮겨간 거리loss = nn.MSELoss()(y_pred, y_train)
# gradient를 초기화
optimizer.zero_grad()
# 역전파: 비용함수를 미분하여 gradient(기울기) 계산
loss.backward()
# W와 bias를 업데이트
optimizer.step()
print(list(model.parameters())) # W: 0.2177, bias: 0.7267
# 반복 학습을 통해 오차가 있는 W, bias를 수정하면서 오차를 계속 줄여나감
# epochs: 반복 학습 횟수(에포크)
epochs = 1000
for epoch in range(epochs + 1):
y_pred = model(x_train)
loss = nn.MSELoss()(y_pred, y_train)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 == 0:
print(f'Epoch: {epoch}/{epochs} Loss: {loss:.6f}')
print(list(model.parameters())) # W: 1.9499, b: 0.1138
x_test = torch.FloatTensor([[5]])
y_pred = model(x_test)
print(y_pred)
3. 다중 선형 회귀
- 여러 개의 입력이 들어가서 한 개의 출력이 나오는 구조
X_train = torch.FloatTensor([[73, 80, 75],
[93, 88 ,93],
[89, 91, 90],
[96, 98, 100],
[73, 66, 70]])
y_train = torch.FloatTensor([[150],[190],[180],[200],[130]])
print(X_train, X_train.shape)
print(y_train, y_train.shape)
# y = W1x1 + W2x2 + ... + b
model = nn.Linear(3,1)
print(model)
optimizer = optim.SGD(model.parameters(), lr=0.00001)
epochs= 10000
for epoch in range(epochs + 1):
y_pred = model(X_train)
loss = nn.MSELoss()(y_pred, y_train)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 ==0:
print(f'Epoch: {epoch}/{epochs} Loss: {loss: 6f}')
print(list(model.parameters())) #W: [0.3478, 0.6414, 1.0172], b:-0.2856
# 93, 93, 93
x_test = torch.FloatTensor([[93, 93, 93]])
y_pred = model(x_test)
print(y_pred)
4. temps.csv 데이터에서 기온에 따른 지면 온도를 예측해보기
df = pd.read_csv('/content/drive/MyDrive/KDT/6. 머신러닝과 딥러닝/Data/temps.csv', encoding='euc-kr')
df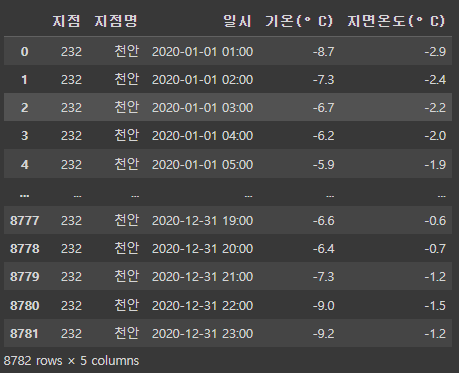
df.isnull().mean()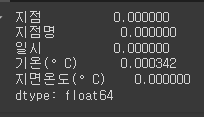
df = df.dropna()
df.isnull().mean()
x_data = df[['기온(°C)']]
y_data = df[['지면온도(°C)']]
x_data = torch.FloatTensor(x_data.values)
y_data = torch.FloatTensor(y_data.values)
print(x_data.shape)
print(y_data.shape)
x_data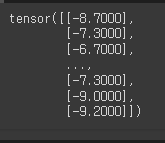
y_data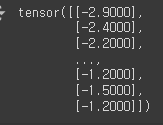
plt.figure(figsize=(8,6))
plt.scatter(x_data, y_data)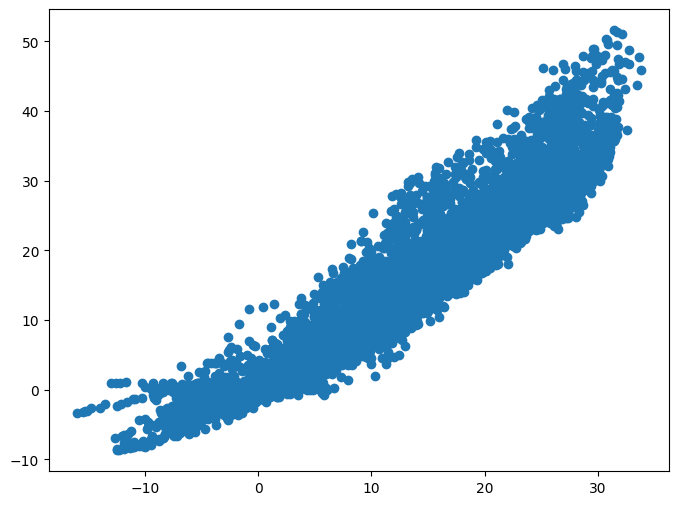
model = nn.Linear(1, 1)
optimizer = torch.optim.SGD(model.parameters(), lr=0.001)
print(list(model.parameters())) # W: -0.5700, b: 0.2403
epochs = 10000
for epoch in range(epochs + 1):
y_pred = model(x_data)
loss = nn.MSELoss()(y_pred, y_data)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 == 0:
print(f'Epoch: {epoch}/{epochs} Loss: {loss:.6f}')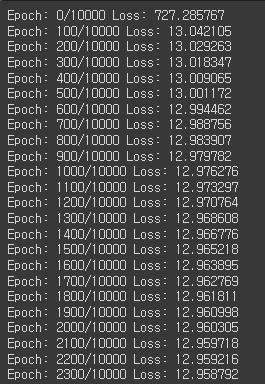
list(model.parameters()) # W: 1.0854, b: 0.8199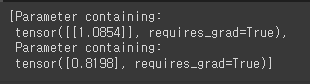
y_pred = model(x_data).detach().numpy()
y_pred
plt.figure(figsize=(8,6))
plt.scatter(x_data, y_data)
plt.scatter(x_data, y_pred)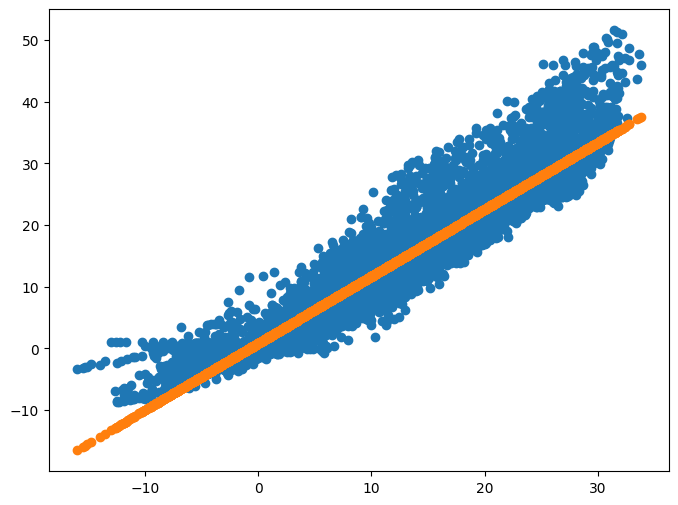
result = model(torch.FloatTensor([[26]]))
result
'Python > 머신러닝(ML)' 카테고리의 다른 글
| Python(31)- 데이터 로더 (0) | 2024.06.20 |
|---|---|
| Python(30)- 파이토치로 논리회귀 구현 (0) | 2024.06.20 |
| Python(28)- 파이토치 (0) | 2024.06.19 |
| Python(27)- Kmeans(K-평균 군집) (0) | 2024.06.19 |
| Python(26)- 다양한 모델 적용 (0) | 2024.06.19 |



